Pi is one of the most fascinating numbers in mathematics due to its irrational and transcendental nature. The simplest calculation of 'pi' is to draw a circle and measure the ratio of the diameter and the circumference which gives us 2-5 decimal digits at best. Although, it may be enough for most practical purposes, calculating digits of pi has been seen as a challenge.

In recent years PIE has been calculated to 130 trilion digits

There are many formulas for computing the value of 'pi'. The most famous of this is 'Machin's formula'.

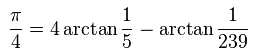
The steps to calculate pi can be summarised in three simple steps:

• Calculate arctan of 1/5 and 1/239
• Multiply arctan of 1/5 by 4 and subtract arctan of 1/239
• Divide the result by 4 to get pi

Using Taylor series, the formula for arctan is as follows:

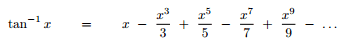
After some refactoring we get a factorial as:

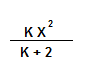
We start with x and continue dividing by the factorial.

This can be written on javascript as:

    function arctan(a) {
      var arctan = createArray();
      var angle = divide(createArray(1), a);
      arctan = addition(arctan, angle);
      var k = 3;
      var sign = 0;
      while (!isEmpty(angle)) {
        angle = divide(angle, a * a);
        div = divide(angle, k);
        arctan = sign ? addition(arctan, div) : subtract(arctan, div); 
        k += 2;
        sign = 1 - sign;
      }      
    }       
  

Once we have the arctan value, rest is just simple arithmetic.

View full code at github

This code is based on Ken ward's work and also of Pascal Sebah